高文琛
在一块土地上展开有序的林业，需要确定树木达到什么树龄时应该进行采伐。法正林的采伐龄称做轮伐期。怎样确定轮伐期，从古至今产生过许许多多的方法。古时曾推崇自然轮伐期，自然轮伐期只是通过对森林自然状态的观察，来确定是否应该采伐，或将树木达到可采伐的年龄，作为伐期龄。
关于自然的伐期龄有两种解释：一是树木达到了自然的成熟或已经到了其生命机能行将结束的年龄；另一种是天然更新最安全的时期，如果是乔木林，就是树木达到了种子成熟并且果实最丰富的树龄，矮林的话就是其萌生力最旺盛的树龄。这样的树龄看似简单明了，其实很不确定，因此不为有序的经济林业所采用。特别是如前者，树木达到了很高的树龄后，其利用价值降低，所以这种方法除非用于防护林、森林公园等以间接利用为目的森林，否则不宜采用。
相对于自然轮伐期稍先进一些的是最大使用价值伐期龄。不过使用这种方法，树龄和最大使用价值的关系很模糊。如果需要达到明显很高的树龄，在现代社会就很难行得通的了。与此类似的有工艺伐期龄，也就是以可获得符合利用目的的木材的树龄为伐期龄。这种确定伐期的方法，从政策上看是可行的。林业经营目的是为了获得特殊利用的木材，适宜采用这种方法，但这个方法也同样完全没有考虑经营成本方面的要素，这也正是这个方法的不足之处。在以生产造纸材为目的时，有时需要采伐树龄很小的森林。总之，这些是旧时代的遗物。
还有一种是以材积收获最大来确定的轮伐期。十八世纪中叶，欧洲出现木材匮乏的情况，要求森林生产出尽可能多的木材，在小面积林地上获取最大的材积就成为最大的经营目标。因此在什么树龄段上能够获得平均最大的材积量就成为确定轮伐期的根本理念。（参阅图250）。即为使
的值最大而去确定U值。其中Mu是伐期获取的材积量，Ma +Mb +…Mq分别是a,b,…q年的间伐所获材积。这也就意味着是伐期平均材积生长最大的一年。可以想得到，过去为了达到这一目的需要将轮伐期拉得很长，后来通过实践知道，如果土壤、气候条件好，实现这个目标所需的时间会大大缩短。这种追求最大材积的方法在薪材、用材的价格都没有变化时代也许适用，但只是在这两种木材的价格高的时候，人们才会去努力生产，争取最大材积。在现代社会忽视价格要素的做法不能称之为好办法。
这样就产生了货币毛收入最大的轮伐期，即以价格取代了前者的材积。除了物质量以外还有了品质的观念，从而更贴近了人们的生活。为了从单位面积上获取最大的货币收入，就要将各材种与单价之积的合计年平均值最大确定为轮伐期。价格的总计是：
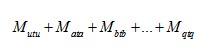其中t为单价 ）
一般可以改写做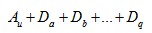
所以在连年作业的场合，对于面积单位来说，以取得 
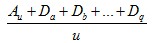的最大来确定u值。即使材积的平均生长量衰减，但只要继续生长总会成为单价高的树木。因此这个轮伐期与前者相比，当然就成了高龄者。这个方法没有将投入的资本考虑进去。资本发生的利息与年俱增。
最大森林纯收益或森林纯贡租的轮伐期，不仅是形式上的货币效益，而且是在扣除各种费用，经计算后以最有利的年份来确定轮伐期的方法。用算数式表现的话，以单位面积
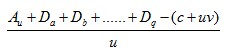的商或在以森林总面积
为最大的年份。其中c是造林费，v是每年发生的费用，F是作业级的面积。
德国云杉的生长曲线()
如果是U个单位面积上有U个龄级分布的法正林，F/u为1，所以前式就成为
从理论上讲，森林平均收入最大额与连年森林纯收入额精确一致，所以u年前后为
原来为
所以
a=材积增长指数
b=价格上涨指数
c=物价上涨指数
因此，该方程式成立，Z（此方法的Weiserprocent）与右项相等时达到伐期龄，因此 Z值较大的期间说明还未成熟。该式如果将间伐收入和造林费省略的话，就变得更简单了，成为
，将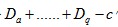
作为对主伐收入的百分比，用d%来表现的话就成为
。
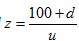根据该方式确定轮伐期，其所用公式只是将扣除部分进行了年平均，而造林费、管理费是一定的，随着木材材积的增加，价格上升，收入也随着增加，所以一般情况是将轮伐期拉长了。与计息的实际计算方法相比，即使立地条件好的林地，其伐期也要推迟三、四十年，地力差的相应更迟一些。轮伐期太长，可能导致森林郁闭度受到破坏，造成土地不良，从而更新困难，而且还可能出现木材腐朽的情况，此外还增加了投资利息的积累。因此这种方法虽然远比前面几种方法优越，但若从经济的角度考虑就不能认为是好的方法了。没有考虑资本利息要素，说明这个方法是不完整的。
弥补这一缺陷的是经济轮伐期（德国学者将此称之为财政轮伐期系属措辞不当）。经济轮伐期指的是纯收入最大的轮伐期，即以获取最高土地纯收入为目标确定的轮伐期。这一方法也因此被称做土地纯收入学说。决定轮伐期的森林期望价即以
的最大化为目标来确定x值。其中m是目前的林龄，p是利率，Beu是土地期望值，V是各种费用的总额。
在同一派中，从该值和费用值的均衡关系导出，成为分母，找出利率，在经济利率以下时作为过熟期的林分，在此以下时作为轮伐期的方法。其导出的路径是
这个W就是普莱斯莱尔（プレスレル）氏所说的指率，表示林木成熟与否的关系。Hkm是现在，即迄至M年所支出的全部费用——费用值，Bk是土地费用值。实查Beu需要收益表，这个公式在实际应用时很麻烦，因此进一步简化为
设
这是尤达依希（ュ-ダィヒ）导出的方程式，因为复杂使用不方便，所以又导出了很多的简化方程
梅尔凯尔(メルケル)方程式
其中
普莱斯莱尔(ブレスレル)方程式
其中
克勒福特(クラフト)方程式
哈伊埃尔(ハイェル)方程式
或
这样计算出来的轮伐期并非恒定不变，由于其所依据要素的变化而未必能表现出真实的经济收入，因此直接应用到实践中去是困难的。利率的变动将引起其值的显著的变动，要对这个利率进行长期预测是非常困难的，同样对将来木材市场的变动也多难以预测。因此即使按照这个方法将轮伐期计算出来，其时期在一定的年度也不是确凿、固定的，而是渐渐到达最高点，然后又渐渐下行，其前后的十年左右，其值无甚大的变化。其曲线如图206所示。
我们不惜花费大量篇幅对轮伐期进行了专门的说明，从而使读者知道轮伐期的确定并非简单的事情。围绕这个轮伐期，反对者与赞成者之间展开了长期的争论。一般说根据最高地贡租的计算的值与根据最高林贡租的计算值相比，得出是短轮伐期。
如果不经过认真的思考就采用这一计算方法，必然招来非议。在德国，多数森林以百分之三的利率计算，其轮伐期为50-60年；如果将利率降得更低，为百分之二或二点五。而且市场好则提高二三十年，但70年乃至80年的轮伐期并不能提供强大的锯材。无论从哪个角度看，这种方法难以行得通，并且还须注意土壤地力的区别。根据土地纯收入学说来确定轮伐期，是不可能在整体的作业级实现，我们需要通过选择不同的土地利用类型和不同的树种，集约地利用土壤地力，在选择轮伐期上，要从实际出发，各个林分别考虑，努力做好森林整体的抚育，增加森林价值。
2013年12月8日